Verschlüsselung und kryptographisches Hashing

In der IT-Sicherheit gehört die Vertraulichkeit zu den Kernkomponenten, die es zu schützen gilt. Es soll also möglich sein eine Nachricht zwischen verschiedenen Geräten austauschen zu können sodass keiner außer diese Geräte die Nachricht verstehen kann. Für dieses Verfahren gibt es verschiedene Verschlüsselungsmöglichkeiten auf die ich in diesem Artikel eingehen werde.

Zusätzlich muss erwähnt werden, dass hier nur auf die Vertraulichkeit einer Nachricht eingegangen wird und nur in einen speziellen Fall auf die Integrität.

Inhaltsverzeichnis

Voraussetzungen für Sicherheitskonzepte

Für Sicherheitskonzepte reicht es nicht aus, das entsprechende Konzept geheimzuhalten. Es gibt genügend Möglichkeiten ein Konzept mithilfe mathematischer Analysen auch ohne Kenntnis der Details zu verstehen und schlussendlich auf die zu schützenden Daten zurückschließen zu können.

Somit muss ein Sicherheitskonzept also das Kerkhoff’sche Prinzip erfüllen.

Ein kryptographisches Sicherheitskonzept muss auch dann sicher sein, wenn der Angreifer alle Details darüber kennt, mit Ausnahme des Schlüssels.

Wenn man das also auf ein Beispiel anwendet, könnte man also Sagen. Es ist möglich herauszufinden wie Google,Meta oder andere Dienste die Kommunikation schützen, jedoch ist es nicht möglich die Übertragungen leserlich zu machen.

Hashing

Es gibt in der Informatik mindestens zwei Einsatzgebiete des Hashings. Einerseits wird es in der Algorithmik zur optimalen Entwicklung von Algorithmen verwendet und andererseits in der IT-Sicherheit zum Schützen von Passwörtern. Ein Beispiel mit SHA3 könnte folgendermaßen aussehen:

testPasswort => SHA3(testPasswort)= 9c8c9d73be7c66bc3401bfc86f5f9ca145c1a707523e73f09…

In der Kryptographie wird eine Hashfunktion mit folgenden 3 Eigenschaften optimal bzw gut genannt.

Urbildresistenz: Es ist nur schwer möglich vom Ergebnis auf den Eingabewert zu schließen
Schwache Kollisionsresistenz: Es ist nur schwer möglich zwei verschiedene Eingabewerte zu finden, di denselben Hashwert haben
Starke Kollisionsresistenz: Anhand von zwei verschiedenen Werten ist es nur schwer möglich ein identisches Urbild zu finden.

Die mathematische Grundlage für eine Hashfunktion bieten Funktionen die nicht stetig differenzierbar sind, was es schwer macht eine Umkehrfunktion zu finden.

Einen Benutzer nun zu authentifizieren funktioniert also nach dem Prinzip, dass seine Eingabe mit der gegebenen Hashfunktion gehasht wird und anschließend mit dem hinterlegten Hashwert verglichen wird. Stimmen die WErte überein, bekommt der Benutzer eine Authorisierung für den entsprechenden Dienst. Mit diesem Verfahren wird sichergestellt, dass der Dienstbetreiber keine Kenntnis über das Passwort hat aber trotzdem auf dessen Echtheit überprüfen kann.

Passwörter und deren Beschreibung

Neben den allgemeinen Aussagen zu Passwörtern und deren Sicherheit kann man diese auch mithilfe der Mathematik beschreiben. Diese Beschreibung ist trivial und gibt uns eine Abschätzung über die Sicherheit und Komplexität eines Passwortes.

Grundlegend gelten für ein sicheres Passwort die folgenden Eigenschaften.

Große Zeichenmenge (a…zA…Z0…9…#…>)
Große Auswahl aus der verfügbaren Zeichenmenge (Möglichst Gleichverteilung der Auswahl)
Viele Zeichen/Langes Passwort (Hohe Entropie)
Kein bereits verwendetes Passwort
Kein Passwort aus einen Dictionary (bspw. die 1000 beliebtesten Passwörter: 1234)

Um ein Passwort jetzt mathematisch zu beschreiben müssen wir ein paar Variablen einführen.

E:=Entropie eines Passwortes

R:=Größe der Menge aller verfügbaren Zeichen

L:=Länge des Passwortes

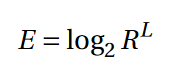
Beispiel:
Verfügbare Zeichen: a…z => R=26
Länge des Passwortes: 3 Zeichen => L=3

E=14,1bits

Mithilfe der Entropie kann man nun berechnen wie lange ein Brutforce-Angriff auf dieses Passwort im Durchschnitt dauern wird.

N:=Anzahl an durchschnittlichen Versuchen

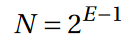
So ergeben sich 8779 Versuche für ein Passwort mit der Entropie von 14,1bit.

Symetrische Verfahren

In diesem Verfahren, möchte man Daten austauschen und dabei die Vertraulichkeit gewährleisten. Dies wird hier mithilfe einer Verschlüsselung umgesetzt bei der ein Schlüssel zum ver- und entschlüsseln verwendet wird. Beide Teilnehmer brauchen also denselben Schlüssel der nur Ihnen bekannt sein darf, weil ansonsten jeder Besitzer des Schlüssels in der Lage ist die Nachrichten mitzulesen.

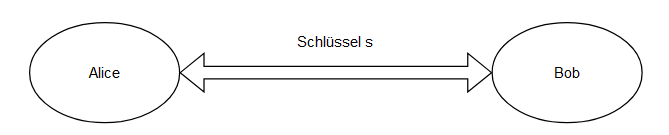
Ein bekanntes Beispiel für ein symetrisches Verfahren ist AES. Wird der Schlüssel sicher ausgetauscht, können beide Teilnehmer darüber miteinander kommunizieren.

x:= Nachricht
k:= Schlüssel
y:= Verschlüsselte Nachricht

y=AES(x,k)

Asymetrische Verfahren

Im Gegensatz zu symetrischen Verschlüsselungsalgorithmen wird hier auf zwei Schlüssel gesetzt. Einmal gibt es den öffentlichen für jeden bekannten Schlüssel, mit dem eine Nachricht verschlüsselt werden kann und dazu gibt es den zweiten geheimen Schlüssel, der nur dem Empfänger bekannt ist. Mit diesem Schlüssel kann er entsprechend die Nachricht entschlüsseln.

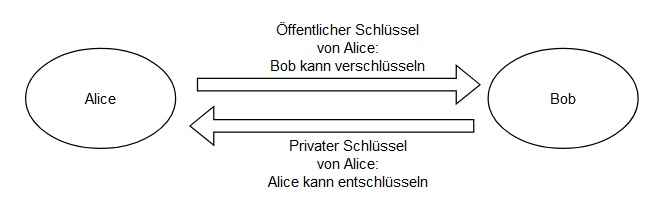
Mit einem asymetrischen Verfahren kann man die Schlüssel für ein symetrisches Verfahren austauschen. Das verhindert aber nicht, einen Man-in-the-middle Angriff, da sich immer noch jemand dazwischen schalten kann und seinen symetrischen Schlüssel weitergeben kann. Um dieses Problem zu beheben kann man auf Zertifikate oder Signaturen zurückgreifen, welche die Intigretät der Daten Sicherstellen.

Beispiel RSA

Ein relativ einfaches Beispiel zum Verständnis asymetrischer Verfahren ist RSA. Als erstes müssen wir uns hier 2 geheime Primzahlen überlegen.

p = 7, q = 11

Damit können wir jetzt den Primfaktor und Q berechnen

N = 7*11 = 77

Q = (p-1)*(q-1) = (7-1)*(11-1) = 60

Als nächstes wählen wir ein öffentliches e und berechnen dazu das inverse d, welches widerrum geheim ist.

Für e gilt 1 < e < Q-1 : e sollte am besten eine Primzahl sein.

e = 47

Mit diesem e können wir nun den erweiterten euklidischen Algorithmus anwenden und schlussendlich unser d bestimmen, welches den Wert d = 23 hat. Zusammengefasst haben wir jetzt alle Zahlen zur Berechnung unserer verschlüsselten Nachricht, wobei der öffentliche Schlüssel durch (e,n) dargestellt wird und der private durch (d,n).

Verschlüsseln wir jetzt die Nachricht x = 8 mithilfe des diskreten logarithmus so erhalten wir folgenden Ausdruck.

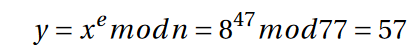
Unsere verschlüsselte Nachricht ist also 57. Wenn wir jetzt die Nachricht wieder entschlüsseln möchten müssen wir folgenden Ausdruck verwenden.

Damit haben wir 8 wieder erhalten, was unsere unverschlüsselte Nachricht war.

In den Quellen habe ich einen Online-Rechner verlinkt, der für eigene Zahlen alles berechnet. Mir ist nicht ganz klar, wie der Rechner sein e bestimmt aber grundsätzlich kommen richtige Ergebnisse raus.

Sonderfall Diffie-Hellman

Neben den bereits beschriebenen Verfahren gibt es auch eins von Diffie-Hellman, mit dem ein Geheimnis ausgetauscht werden kann ohne jemals dieses Geheimnis jemals übertragen zu müssen. Dieses Verfahren kann für einen sicheren Austausch des Sessionkeys eines symetrischen Verfahrens verwendet werden.

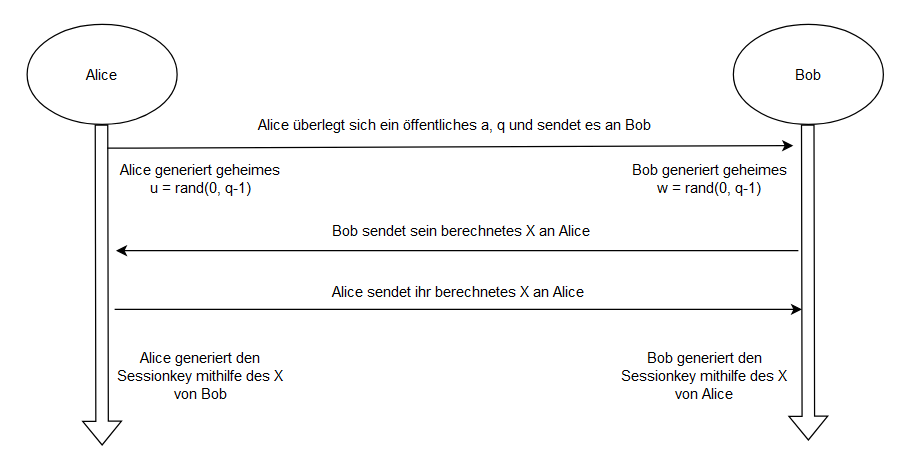
Schauen wir uns jetzt eine Beispielrechnung an. Wir nehmen die folgenden Werte: a = 5, q = 97. Das geheime u für Alice ist u = 36 und das geheime w für Bob ist w = 15.

Als erstes berechnen wir beide X für den jeweils anderen.

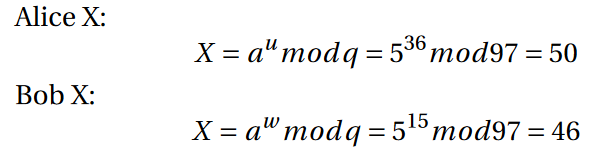
Im nächsten Schritt berechnen beide für sich mithilfe des X vom jeweils anderen das Geheimnis, welches durch den Sessionkey dargestellt wird. Wenn die Berechnungen vorher richtig waren, so wird für beide das jweils selbe Ergebnis rauskommen.

33 ist also das Geheimnis, was sich beide berechnet haben, jedoch nie übertragen haben. Somit kennen beide den Session-Key.

Quellen

https://www.browserling.com/tools/sha3-hash (17.2.2024, 11:43)

https://tools.justus-d.de/rsa/ (18.2.2024, 15:14)