Advanced Datastructures

This article deals with advanced datastructures and algorithms about Pairing-Heaps, Fibonnaci-Heaps, Node-Potentials and Strongly connected components. You will find a table with every datastructure listed below and a link to my github-account with some of them implemented in C/C++ or Java.

Pairing Heap

Pairing heaps are as the name suggests heaps with some advantages compared to e.g Binary Heaps. It is often called, simplified fibonaccie heap. This Heap goes with the property of a min heap. It has a root element. This element also has the min property.

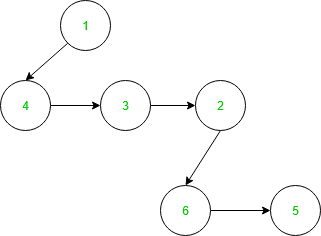
Insert-Item

To insert elements into the tree, we need to union the existing tree(s) with the new tree having the single element we’d like to add. For this reason the insert method just executes the newTree() or union() operation on both trees as parameter.

The runtime of this operation is Θ(1).

proc insert(h:Handle)
      newTree(h)

proc newTree(h:Handle)
      forest = forest U {h}
      if elem(h) < minPtr then
          minPtr:=h

As mentioned before, this method just creates a new tree. It’s not supposed to insert the element into an existing tree as this would take more time.

Decrease-Key

Set the k := key(*h) of *h := Handle to a given value k and cut if our element is not the root element. The runtime of this operation is O(logn)

In general speaking this will lower the value of a given Element and set it to the right position in the heap structure.

proc decreaseKey(h:Handle, k:Key)
    key(h):=k
    if h not root then
        cut(h)

Delete-Min

Set the forest without a given handle. Furthermore, create new trees for each child of the min and perform pair-wise union. Finally update the minPtr.

In gerneral speaking this operation deletes the minimum valued element which is given by a direct pointer called minPtr. After its deleted we insert each element of the tree without a minimum element into the forest meaing we create a tree for each element. Finally we perform a pair-wise union operation to create one tree again.

Runtime of this operation is O(logn)

proc deleteMin()
     m:=minPtr
     forest=forest\{m}
     foreach child of m do
        newTree(h)
        pair-wise union
     update minPtr

Merge

This operation merges two heaps and set the global minPtr.

Perform union of all elements int both heaps and delete the second heap as its not needed anymore and return the first heap.

The runtime of this operation is Θ(1)

proc merge(hp:PHeap)
     if minPtr > hp.minPtr then
        minPtr = hp.minPtr
     forest = forest U hp.forest
     hp.forest = {}                //Empty the forest meaning the second param.

Fibonacci Heap

This kind of heaps is a faster implementation of the pairing heap and many faster operations when compared to binary heaps such as insert, union, decrease-key,…

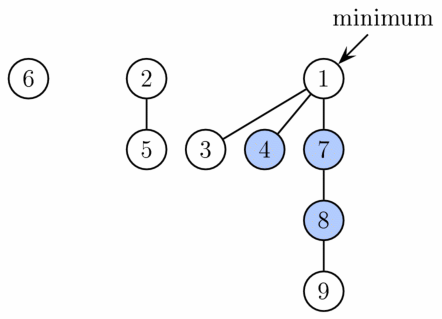
Fibonacci Heaps are often used if the number of extractMin and delete-calls are small. For example this is the case in shortest path problem.

On wikipedia you’ll find a good summary of Fibonacci-heaps as i only summarize the runtimes of the different operations.

Operation	Runtime	Notes/additional information
insert	Θ(1)
getMin	Θ(1)
extractMin	O(logn)*	amortized
decreaseKey	Θ(1)*	amortized
remove	O(logn)*	amortized
merge	Θ(1)

Node Potentials

The sum of all edges/weights on the path to the node.

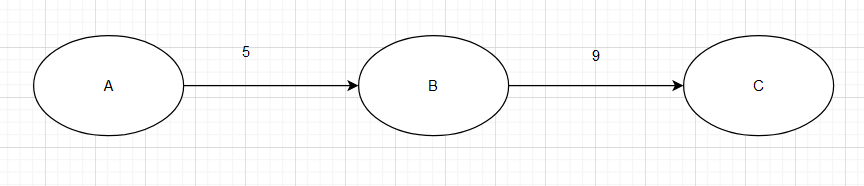
In the graph above the node potentials look like:

• pot(A)=0
• pot(B)=5
• pot(C)=5+9=14

Using node potentials some problems will become easier to solve. For example the All-Pair-Shortest-Path problem has a runtime of O(nm+n²logn) which is significantly faster compared to Bellman-Ford with O(n²m)

Bucket Queue

Strongly Connected Components (SCC)

A graph can be contracted and contains SCC when the following statement is valid:

Given a graph g=(V,E) with u,v∊V and p,q= a path from one to another node
∃p->q ⋀ ∃q->p : p = {u,...,v} ⋀ q={v,...,u}

The statememt above sais there is a SCC if a path from u to v exists and a path from v to u exists. Beside the start and the end node the paths can be disjoint. The goal behind SCC is to summarize nodes to one node if they have the same reachable neighbors.

The following graph:

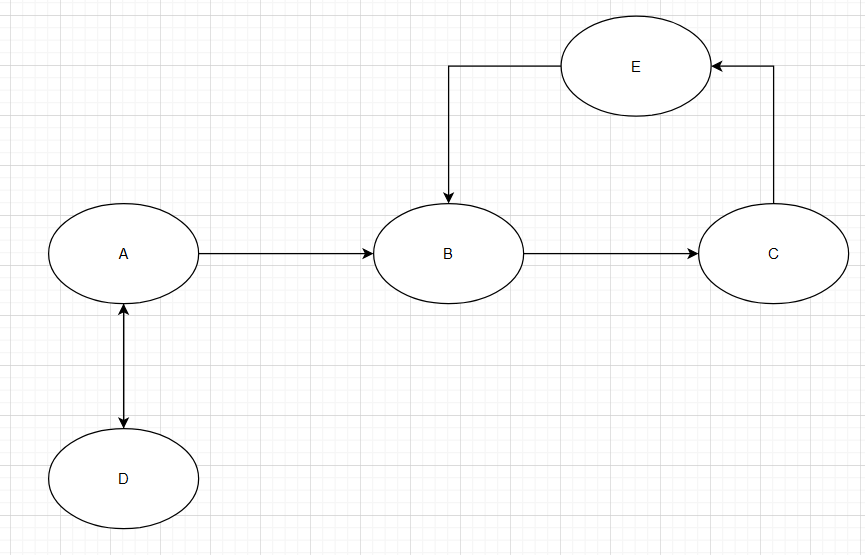
has 2 SCC and its contracted version looks like this.

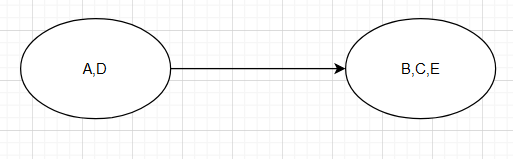
For contracted graphs you have a few preconditions to decide on wether its the final graph or not.

• The contracted graph is acyclic

Sources

https://en.wikipedia.org/wiki/Pairing_heap (28.12.2023, 6:47)

https://www.geeksforgeeks.org/pairing-heap/ (28.12.2023, 14:45)

https://www.baeldung.com/cs/min-heaps-decrease-key (25.01.2024, 11:08)

https://de.wikipedia.org/wiki/Fibonacci-Heap (25.01.2024, 11:19)