Computer graphics
Computer graphics is a field within computer science that deals with the display of graphical elements on monitors and the processing of the corresponding data. The area of 3-dimensional representation and corresponding processing is particularly important because the goal is to render a 3D scene on a 2D screen.
Table of Contents
Color and Color-spaces
When color is displayed on a screen, it is first necessary to define which color is being discussed. The goal is to ensure that everyone perceives the same color, at least in terms of its numerical representation.
From physics, we know colors and light as electromagnetic waves with different wavelengths. A large wavelength corresponds to light with low energy, and a small wavelength corresponds to light with high energy.
When we want to process colors on a computer, we need to imagine a metric through which we define our colors. The simplest way is to use the existing technology directly. A typical screen can display RGB (red, green, blue) and the colors mixed from them. Therefore, we could say that we can represent every color with three components. This is also the assumption of Grassmann. He established a law in which he claims that this is exactly possible.
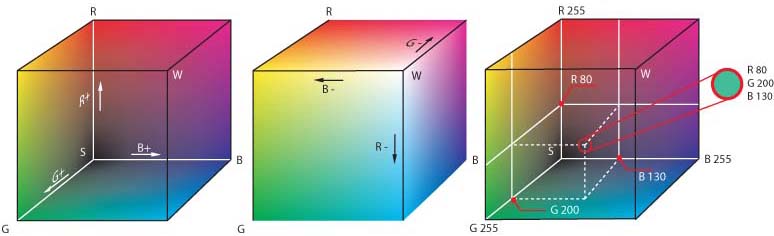
RGB is the best-known and most commonly used color space. However, both mathematically and empirically, it can be observed that not all colors can be represented within this space. For this reason, additional color spaces have been developed to enable the display of colors that are not included in RGB.
CMY(K) (Cyan, Magenta, Yellow, Black) is a color model used in printers because it allows for ink savings. Naturally, it is possible to convert from RGB to CMY(K) and display a color in the corresponding different model.
A translation into the respective other color space looks as follows:

RGB = [0,...,255]³ CMYK = [0,...,1]⁴
R' = R/255
G' = G/255
B' = B/255
Convertion to CMYK:
K = 1-max(R',G',B')
C = (1-R'-K)/(1-K)
M = (1-G'-K)/(1-K)
Y = (1-B'-K)/(1-K)
Additive and substractive color mixing
In additive color mixing, the three primary colors red, green, and blue are mixed together to produce all the colors that we can display on an ordinary computer screen.
Subtractive color mixing is used for colors associated with materials (such as printing, ink, etc.).
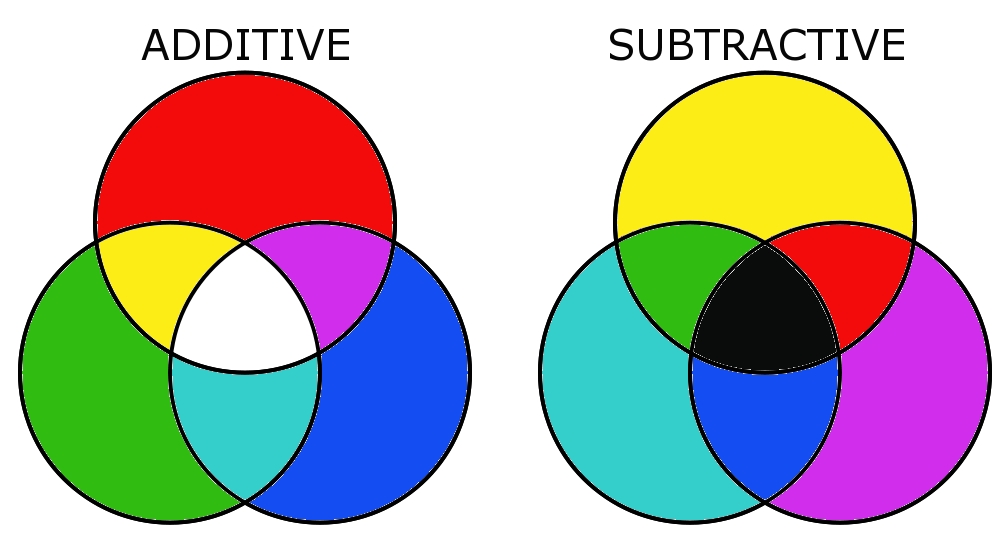
Different types of displays
For color representation, the technology used in the monitor also matters. This may not be particularly relevant for everyday use, but if you work in a creative field such as photography, 3D design, or video editing, you should carefully consider which monitor to use, as the appearance of an image can vary between different screens.
Simply lowering the brightness on your own screen can affect color perception.
Today, there are many different types of screens. Types like LCD or OLED work with pixels and the RGB color space, while a vector monitor uses electron beams, offering an infinitely high resolution and a color space similar to RGB.
Frame buffer
Moving from the representation of various colors to the technical aspect, let’s examine a problem that definitely arises if the data is not intercepted in advance.
For every image we want to display on a screen, whether a single image or part of a video, we need to calculate each pixel and pass it to the GPU to be displayed. These calculations take time. If we take the time to calculate this „live,“ it will result in a lower FPS (Frames per Second). If this number falls below ~25, the eye no longer perceives a continuous video and detects flickering instead.
This problem can be resolved by performing the calculations in advance and storing them temporarily. This is where the frame buffer comes in.
class FrameBuffer {
width := Display width
height := Display height
buffer := 2D Array of int's
proc recalculate(color)
for x to width do
for y to height do
buffer[x][y] = color
}Aliasing and jaggies
When having a finite resolution one will encounter the problem of aliasing effects and so called „jaggies“. Best known on older systems there are stair like lines on the border of virtual objects.

With the development of the last years, these effects are mostly solved with anti aliasing methods like SAA (Supersampling), Adaptive supersampling or prefiltering.
Ray tracing and Rasterization
Ray tracing is a technique to simulate rays and their path to an object in scene. By calculating the intersections of the rays you’ll determine which object is in front or how shadows and other effects can be shown to the user.
Important here, is that you trace the rays „backwards“ meaning your rays start at the Camera and hit eventually the light src. Using this direction you have a great increase in Runtime performance.
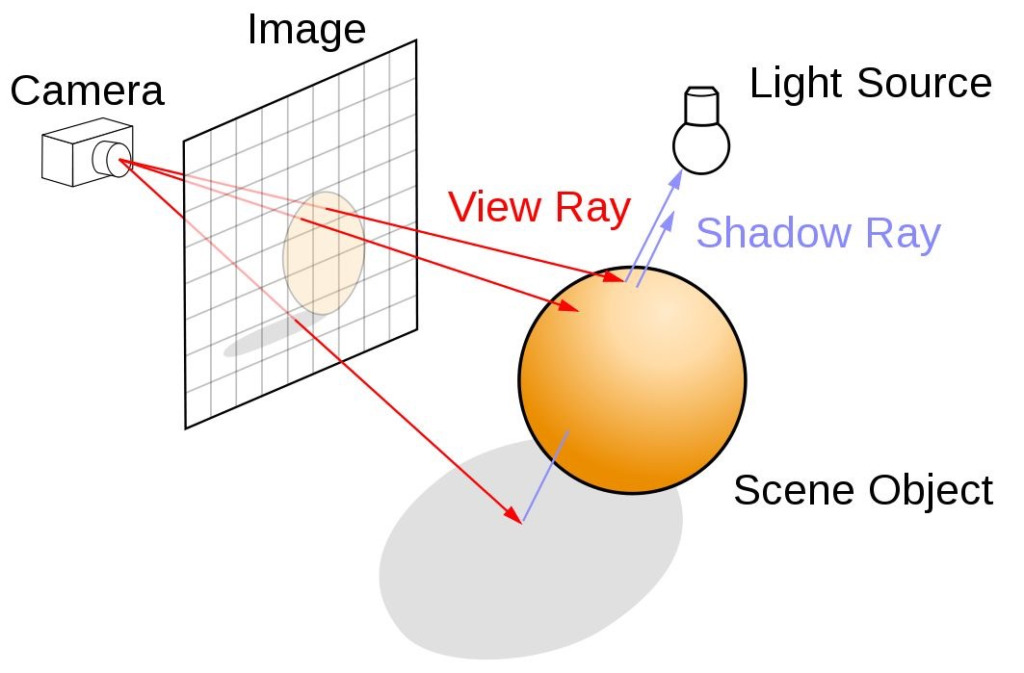
Rasterization on the other side, projects the visible part of the scene onto a 2D plane and determines the objects in front by checking each pixel and their depth value
Virtual scene and coordinate systems
Virtual lights
Let’s look at a scene that we can equip with different types of lights. Each variant has its own advantages and disadvantages. Summarized, the possible options for light sources are as follows:
Phong and Gouraud shading
Render-equation
Lighting conditions in computer graphics can be described by an equation. This equation is called the rendering equation and is one of the most important fundamentals in CG.
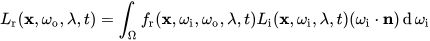
This equation describes the amount of light coming from a point x at angle ω to the observer. The emission is taken into account, and the reflection or scattering at point x is calculated using the Bidirectional Reflection Distribution Function (BRDF) or Bidirectional Scattering Distribution Function (BSDF), considering the angles. This can be done either as an integral or discretely.
Transformations
Source
https://de.wikipedia.org/wiki/Farbenlehre (16.7.2024, 10:21)
https://de.wikipedia.org/wiki/RGB-Farbraum (16.7.2024 10:23)
https://en.wikipedia.org/wiki/Jaggies (17.7.2024, 11:31)
https://en.wikipedia.org/wiki/Rendering_equation (29.7.24, 20:05)