Rekurrenzen und Master-Theorem
Das nächste Thema im Bereich der Algorithmusentwicklung oder -beschreibung behandelt Rekurrenzen. Diese stellen ein mathematisches Konzept dar, um Laufzeiten rekursiver Algorithmen zu beschreiben. Insbesondere werden mit Hilfe von Rekurrenzen Algorithmen beschrieben, die dem Prinzip „Teile und herrsche“ folgen. In diesem Artikel werde ich detailliert erläutern, was dies bedeutet und wie man die Laufzeit solcher Algorithmen bestimmen kann.
Für diesen Algorithmus ist es sinnvoll, wenn bereits Wissen zur O-Notation vorhanden ist. Andererseits habe ich hier einen Artikel zur O-Notation und Laufzeitanalyse von Algorithmen.
Themen
Rekurrenzgleichungen
Eine Rekurrenzgleichung hat folgende Struktur.
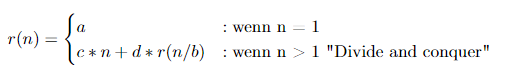
Sie beinhaltet die 4 Konstanten a,b,c,d die alle positiv sein müssen. N ist genau wie bei der Laufzeitanalyse die zu lösende Problemgröße. Im Basisfall bietet diese Funktion eine konstante Laufzeit, welche der Konstante a entspricht. Für alle weiteren n gibt es die rekursive Teilfunktion.
Master-Theorem
Das Master-Theorem ist eine allgemeine Form, die mathematisch bewiesen wurde und zur Lösung von Rekurrenzgleichungen anwendbar ist. Die Herleitung des Master-Theorems ist relativ einfach und gehört oft zum Bestandteil einer Algorithmen-Vorlesung an Universitäten. Hier beschränken wir uns aber nur auf die richtige Verwendung.
Wie im ersten Teil des Artikels erwähnt kann man Rekurrenzgleichungen mithilfe vom Master-Theorem einfach lösen. Für das Theorem legen wir folgendes fest. Es seien a,b,c,d ∈ (0, ∞) Konstanten. Mit dieser Vorgabe können wir nun das Master-Theorem zur Lösung unserer Gleichung anwenden. Das Master-Theorem hat somit folgende Struktur.
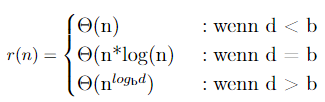
Wenn wir also unsere gegebenen Werte für d und b einsetzen, können wir also direkt ablesen, welche Laufzeit der Algorithmus hat. Dafür müssen wir somit nicht einmal etwas berechnen!
Beispiele
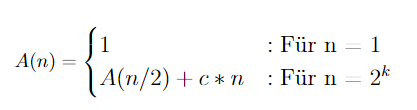
Aufgabe: Zeige mithilfe des Master-Theorems welche Laufzeit die oben gezeigte Rekurrenz aufweist.
Lösung: Schauen wir uns nochmal den Aufbau von Rekurrenzen an. Wenn wir die allgemeine Form betrachten sehen wir, dass jede Zahl hier durch eine entsprechende Variable ersetzt werden kann
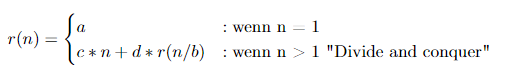
Somit haben wir also folgende Variablen: a = 1, b = 2, c=c (kein konkreter Wert), d = 1
Jetzt haben wir alle Variablen einmal aufgeschrieben und verwenden jetzt das Master-Theorem um die Aufgabe zu lösen.
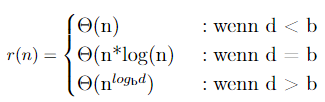
Im Master-Theorem sehen wir, dass für die Laufzeitanalyse nur d und b entscheidend sind. Somit schreiben wir einmal d und b gegenüber und schauen welcher Wert größer ist.
d = 1 und b = 2 => d < b = 1 < 2 => Θ(n)
Durch einfaches ablesen konnten wir jetzt feststellen, dass unser Algorithmus, der mit dieser Rekurrenz beschrieben wurde, eine Laufzeit von Θ(n) hat.
Quellen
https://hpi.de/friedrich/teaching/units/rekurrenzen-und-master-theorem.html (23.6.23 17Uhr)
https://en.wikipedia.org/wiki/Master_theorem_(analysis_of_algorithms) (23.6.23 17:30Uhr)